 更多“证明:域F上多项式环F[x]的每个理想都是主理想.”相关的问题
更多“证明:域F上多项式环F[x]的每个理想都是主理想.”相关的问题
第1题
设a1,a2,...,an是数域F中互不相同的数,b1,b2,...,bn是数域F中任一组给定的数,用Cramer法则证明:存在唯一的数域F上,次数小于n的多项式f(x),使f(ai)=bi。
设a1,a2,...,an是数域F中互不相同的数,b1,b2,...,bn是数域F中任一组给定的数,用Cramer法则证明:存在唯一的数域F上,次数小于n的多项式f(x),使f(ai)=bi。
点击查看答案
第2题
设为开域,f:D→Rm为可微函数.利用定理23.14证明: (1) 若在D上f'(x)恒为0矩阵(零矩阵),则f(x)为常向量函
设
(1) 若在D上f'(x)恒为0矩阵(零矩阵),则f(x)为常向量函数;
(2) 若在D上f'(x)≡c(常数阵),则f(x)=cx+b,x∈D,b∈Rm.
第3题
令Mn(F)是数域F上全体n阶矩阵所成的向量空间。取定一个矩阵A∈Mn(F)。对于任意X∈Mn(F
令Mn(F)是数域F上全体n阶矩阵所成的向量空间。取定一个矩阵A∈Mn(F)。对于任意X∈Mn(F
点击查看答案
),定义σ(X)=AX-XA。已知σ是Mn(F)的一个线性变换。设

是一个对角矩阵。证明,σ关于Mn(F)的标准基{Eij|1≤i,j≤n}的矩阵也是对角矩阵,它的主对角线的元素是一切ai-aj(1≤i,j≤n)。
第4题
设α是A的对应于特征值λ0的特征向量,证明:(1)α是Am的对应于特征值的特征向量;(2)对多
设α是A的对应于特征值λ0的特征向量,证明:(1)α是Am的对应于特征值的特征向量;(2)对多
点击查看答案
设α是A的对应于特征值λ0的特征向量,证明:
(1)α是Am的对应于特征值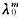 的特征向量;
的特征向量;
(2)对多项式f(x),α是f(A)的对应于f(λ0)的特征向量。
第5题
证明:若f'x(x,y)与f'y(x,y)在矩形域D有界,则函数f(x,y)在D一致连续.
证明:若f'x(x,y)与f'y(x,y)在矩形域D有界,则函数f(x,y)在D一致连续.
点击查看答案
第6题
设g(x)是系数属于域Zp(p是素数)的一个多项式.证明: [g(x)]p=g(xp).
设g(x)是系数属于域Zp(p是素数)的一个多项式.证明: [g(x)]p=g(xp).
第7题
设f(x1,x2,…,xn)是数域F上一个,x元齐次多项式,证明:如果g(x1,x2,…,xn)=g(x1,x2,…,xn)h(x1,x2,…,xn),则g,h也
设f(x1,x2,…,xn)是数域F上一个,x元齐次多项式,证明:如果g(x1,x2,…,xn)=g(x1,x2,…,xn)h(x1,x2,…,xn),则g,h也是,n元齐次多项式.
第9题
证明:若函数f(x)在[a,+∞]有连续的导函数f'(x),且无穷积分都收敛,则
证明:若函数f(x)在[a,+∞]有连续的导函数f'(x),且无穷积分都收敛,则
点击查看答案
证明:若函数f(x)在[a,+∞]有连续的导函数f'(x),且无穷积分
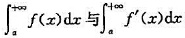 都收敛,则
都收敛,则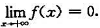


 如果结果不匹配,请
如果结果不匹配,请 

















