题目内容
（请给出正确答案）
[主观题]
设g（x)是系数属于域Zp（p是素数)的一个多项式．证明： [g（x)]p=g（xp)．
设g(x)是系数属于域Zp(p是素数)的一个多项式．证明： [g(x)]p=g(xp)．
查看答案
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
设g(x)是系数属于域Zp(p是素数)的一个多项式．证明： [g(x)]p=g(xp)．
如果结果不匹配，请 联系老师 获取答案
更多“设g（x)是系数属于域Zp（p是素数)的一个多项式．证明： …”相关的问题
设R是有单位元的整环(可换、无零因子)．证明： 1)若char R=∞，则R有子环与Z同构； 2)若char R=p(p是素数)，则R有子环与Zp同构．
设f(x1，x2，…，xn)是数域F上一个，x元齐次多项式，证明：如果g(x1，x2，…，xn)=g(x1，x2，…，xn)h(x1，x2，…，xn)，则g，h也是，n元齐次多项式．
设函数f(t，x)在平面上的条形区域G：a＜t＜b，｜x｜＜∞上连续，φ1(t)，φ2(t)是方程
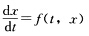过同一点(t0，x0)∈G的两个解，φ1(t)≤φ2(t)．证明域G中介于φ1(t)，φ2(t)间的部分被方程过点(t0，x0)∈G的解充满．
设f(x)是一个多项式，用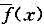
表示把f(x)的系数分别换成它们的共轭数后所得多项式。证明：
(i)若g(x)|f(x)，那么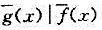
;
(i)若d(x)是f(x)和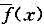的一个最大公因式，并且d(x)的最高次项系数是1，那么d(x)的最高次项系数是1，那么d(x)是一个实系数多项式。
设p是素数，a是整数，则当p|a时，gcd(p，a)=p；当p≥a时，gcd(p，a)=1．
令V是实数域R上一个三维向量空间，σ是V的一个线性变换。它关于V的某一个基的矩阵是
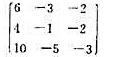
(i)求出σ的最小多项式p(x)，并把p(x)在R[x]内分解为两个最高次项系数是1的不可约多项式p1(x)与p2(x)的乘积;
(ii)令Wi={ξ∈V|pi(σ)ξ=0}，i=1，2。证明，Wi是σ的不变子空间，并且V=W1⊕W2;
(iii)在每一子空间Wi中选取一个基，凑成V的一个基，使得σ关于这个基的矩阵里只出现三个非零元素。
