 更多“设Y是赋范空间X的子空间,g∈Y'且f∈X'…”相关的问题
更多“设Y是赋范空间X的子空间,g∈Y'且f∈X'…”相关的问题
第1题
设Y是赋范空间X的有限维真子空间。证明在X中存在x1使得‖x1‖=1且d(x1,Y)=1,即Riesz引理在r=1时成立。
设Y是赋范空间X的有限维真子空间。证明在X中存在x1使得‖x1‖=1且d(x1,Y)=1,即Riesz引理在r=1时成立。
第2题
设X和Y是赋范空间。E是X的有界完备凸子集,是满足下列条件的连续映射F:X→Y的集合:对0<r<1及x,y∈E, F(rx+(1-r
设X和Y是赋范空间。E是X的有界完备凸子集, 是满足下列条件的连续映射F:X→Y的集合:对0<r<1及x,y∈E,
是满足下列条件的连续映射F:X→Y的集合:对0<r<1及x,y∈E,
F(rx+(1-r)y)=rF(x)+(1-r)F(y)
证明 在E上一致有界当且仅当它在E上逐点有界。
在E上一致有界当且仅当它在E上逐点有界。
第5题
设X和Y是赋范空间,F:X→Y是线性的,证明下列陈述是等价的: (a)F是连续的。 (b)F映X中的柯西列到Y中的柯西列。
设X和Y是赋范空间,F:X→Y是线性的,证明下列陈述是等价的:
(a)F是连续的。
(b)F映X中的柯西列到Y中的柯西列。
(c)F映X中的收敛列到Y中的收敛列。
第7题
设X是Banach空间,Y是赋范空间,对n,m=1,2,…。设Fmn∈BL(X,Y)若对每个m≥1,存在X中的xm使得 证明存在X中的x使
设X是Banach空间,Y是赋范空间,对n,m=1,2,…。设Fmn∈BL(X,Y)若对每个m≥1,存在X中的xm使得
证明存在X中的x使得

第8题
若X是无穷维赋范空间,证明以下结论: (a)存在单的不连续的线性映射F:X→X (b)存在X上不连续的线性泛函。 (d
若X是无穷维赋范空间,证明以下结论:
(a)存在单的不连续的线性映射F:X→X
(b)存在X上不连续的线性泛函。
(d)对任意的赋范空间Y≠{0},存在不连续的线性映射F:X→Y


 如果结果不匹配,请
如果结果不匹配,请 
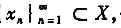

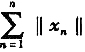
 收敛.
收敛.
















